A Vector Error Correction Model (VECM) can be seen as an extension of a VAR model. Where a VAR model requires all the included variables to be stationary, a VECM does not. Instead, it requires the variables to be cointegrated, meaning that there exists a linear combination of them which is stationary. These linear combinations can for k time series y1,...,yky1,...,yk be written as
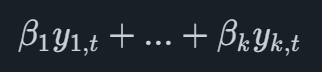
where the β terms are coefficients and yi,t is the observations of variable i at time t.
The first step towards fitting a VECM model is to determine if there is any cointegration present in the data. This is commonly done using the Johansen test which determines the number of stationary linear combinations. These are referred to as cointegration vectors and the number of them as determined by the Johansen test is usually denoted with the letter r.
From the article on VAR models we have the equations which describes each variable as a function of its own lags and the lags of the other variables as
where the error terms εt is the part of ytyt which is not explained by the model. In the model there are k equations, one for each variable. The terms al are matrices containing the coefficients at lag l in all equations and yt is a vector of the observations of all variables at time tt.
In a VECM model, the VAR process is modeled on the first difference transformation of the variables, denoted δtδt at time tt. The full VECM model can now be written as
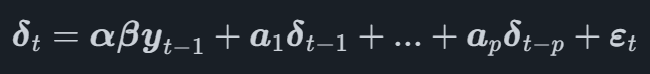
where β is a matrix which contains the coefficients from the cointegration vectors and αα is a matrix which contains the adjustment vectors for the cointegration vectors.
Studying the equation we can see that the first difference of the time series is modeled as a function of the cointegration vectors and the lags of each time series.
To fit a VECM model, the first task is to select the order (i.e. the number of lags) of it. In Indicio this is done by fitting VAR models of order 1,...,pmax1,...,pmax where pmaxpmax is the maximum number of lags selected by the user. The one that fits the data the best according to Akaike's Information Criterion (AIC) is selected, this favors a simple model over a more complicated one, but still accounts for a good model fit.
After the lag order is selected, the Johansen test is applied to determine the cointegration rank r. With these parameters selected, the model is fitted to the data.
We are an automated forecasting software that bridges the latest statistical models from academia with the specific leading indicators in an organization's market environment. Helping your organization achieve the highest forecast accuracy.
© 2025 Indicio Technologies All Rights Reserved