Vector Autoregressive (VAR) models are used to capture the relationship between multiple time series and can be seen as a multivariate generalization of autoregressive (AR) models (see Advanced: ARIMA). As such a VAR model can describe a complex set of linear relationships between a set of variables. A VAR model requires all the included variables to be stationary, in cases where one or more variables are not stationary, it is common to take the first difference to achieve stationarity.
To define a VAR model, we first denote the number of variables as k and the number of lags used as p. The number of lags is often referred to as the order of the model.
By writing the different time series included in the model as Yi we can write the vector of kk variables as time t as
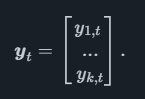
A VAR model will have one equation for each variable, describing it as a function of the lags of all the kk variables. For each lag l a coefficient vector ai,l defines how this lag affects the variable Yi which the equation belongs to.
We can now write the equation for each variable as
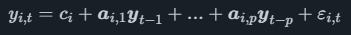
where ci is a constant and the error term εi,t is the part of yi,t which is not explained by the model. In the model there will be k equations, one for each variable. All the equations can together be written as
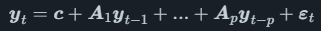
where the Ai terms are now matrices where the coefficients for all equations are present and both the error term and constant are vectors. Also note that the vector yt on the left hand side is a vector of all variable observations at time t.
In Indicio, it is possible to add events to a forecast, these are modeled as exogenous variables which means that they follow a predetermined path, even in the unknown future periods of the forecast. A VAR model supports these by adding them on the right hand side of each equation, meaning that the current value is not only a function of its own and the other variables, past lags, but also of the contemporary values of the exogenous variables. If an extreme event had an effect on the data, an event at this point in time will allow the model to assign the part of the data that is not explained by the model using the event, giving the model a better opportunity to describe the time series as it would have looked without the event.
To fit an VAR model, the first task is to select the order (i.e. the number of lags) of it. In Indicio this is done by fitting models of order 1,...,pmax1,...,pmax where pmax is the maximum number of lags selected by the user. The one that fits the data the best according to Akaike's Information Criterion (AIC) is selected, this favors a simple model over a more complicated one, but still accounts for a good model fit.
We are an automated forecasting software that bridges the latest statistical models from academia with the specific leading indicators in an organization's market environment. Helping your organization achieve the highest forecast accuracy.
© 2025 Indicio Technologies All Rights Reserved