VARMA

The Vector Autoregressive Moving Average (VARMA) model is a multivariate generalization of a univariate ARMA model (see Advanced: ARIMA). Just like the ARMA part of an ARIMA model, a VARMA model has both an Autoregressive (AR) and Moving Average (MA) part, both which may have a different order. Therefore, a VARMA model is said to be of order (p,q) when it has pp AR terms and qq MA terms.

Say that we have three variables, one of which we are interested in forecasting. The AR part of a VARMA model is very similar to a VAR model in that it describes the next value of each variable as a function of the p lags of itself and the two other variables. A VARMA model is a bit more sophisticated. It's like a VAR model with an added twist. In addition to considering the past values of the variables, a VARMA model also considers the past forecast errors of those variables. Forecast errors are the differences between the actual values and the values predicted by the model. So, a VARMA model takes into account not just the historical values of the variables but also how well the model has done in predicting them in the past.

To more formally describe a VARMA model, we begin by defining some numbers. If we have k variables Y1,...,YkY1​,...,Yk​, a VARMA model of order (p,q) can be written as

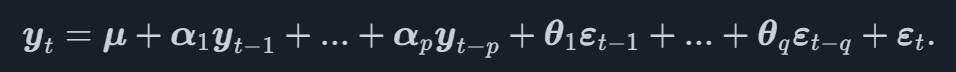
Where yt​ is a vector of the observations of all time series at time tt, the αl​ terms are the vectors of AR coefficients at lag l, θj​ denote the vectors of MA coefficients at each step in the MA process j. Finally there is also the error vector εt​ at time t, containing the part of the data which is not explained by the model.

Suppose you are tasked with predicting stock market returns and interest rates. In the context of a VAR model, historical stock market return values and past interest rate levels are used to predict their future values. However, imagine a sudden geopolitical event occurs that significantly impacts both the stock market and interest rates, an event not accounted for in the historical data. The VAR model might struggle to accurately forecast the market reaction and interest rate adjustments prompted by this unexpected event, as it lacks prior instances of such occurrences.

Here, a VARMA model offers an advantage. If the VARMA model had previously underestimated market reactions and interest rate changes during similar unforeseen events, it acknowledges these past forecasting errors and adjusts its future predictions accordingly. By learning from its past forecasting inaccuracies, the VARMA model becomes more adept at handling unanticipated market shifts and improves the precision of its predictions.

In essence, the VARMA model is particularly suitable for situations in finance and market intelligence where intricate relationships or latent patterns within forecast errors could exist. This ability enables the model to enhance its predictions by drawing insights from its prior misjudgments and progressively refining its forecasting performance over time.

‍