VARX Lag Group Lasso

The VARX Lag Group Lasso model is an extension of the VARX Lasso model which instead of a regular Lasso penalty is using a Group Lasso penalty, grouping the coefficients in the equation per lag in the model.

The Group Lasso requires the coefficients to be divided into groups. Each group of coefficients l is denoted A(l) and the number of groups m. The group lasso penalty is then written as

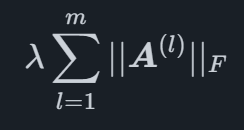
where and ∣∣X∣∣2​ is the Frobenius norm of X which is defined as

‍

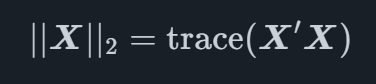
for a matrix X, where the tracetrace is the sum of diagonal entries of a square matrix. The benefit of this type of penalty is that it is able to shrink whole groups of coefficients to zero, leaving other groups with non-zero values.

The effect of applying a group lasso where the coefficients of each lag belong to a group to a VAR model is that important lags will be allowed to remain in the model, whereas not important ones may be penalized away completely. This produces a model where only lags which are useful when producing a forecast are kept, leaving it up to the model to select which lags are important. A downside to this strategy is that it is not always the same lags that affect all the variables.