VARX Elastic Net

The VARX Elastic Net model is an extension of the VARX Lasso model which instead of a regular Lasso penalty is using a Elastic net penalty. The Lasso penalty is defined as

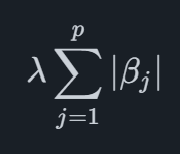
where the penalty depends on the sum of absolute values of the coefficients. In high-dimensional datasets with correlated variables, Lasso tends to select one variable while ignoring others that are correlated with it. Related to Lasso we have Ridge regression which uses the similar penalty

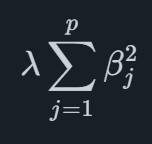
where the absolute values are replaced by the square of the coefficients. This has the effect of shrinking coefficients towards zero, just like with a Lasso penalty. Ridge regression mitigates multicollinearity by shrinking coefficients toward zero without setting any to exactly zero. While it addresses multicollinearity, it does not inherently provide variable selection.

Putting these two penalties together, we get the Elastic Net penalty as

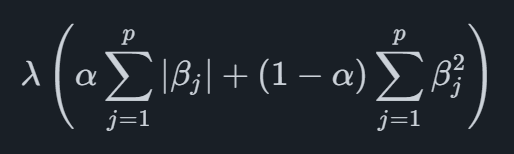
where the parameter αα is used to determine the mixture between Lasso and Ridge regression. This combination allows Elastic Net to handle multicollinearity like Ridge while encouraging sparsity like Lasso. It strikes a balance between variable selection and preserving correlated predictors.

In summary, Elastic Net is preferred over Lasso or Ridge regression when dealing with high-dimensional datasets containing correlated variables. It strikes a balance between variable selection and multicollinearity mitigation, making it a versatile choice for scenarios where both concerns are relevant. However, the choice ultimately depends on the specific characteristics of the data.