Neural Net

Neural networks aim to imitate the way the neurons in a human brain works. The main benefit over a linear model is that neural networks can model more complex non-linear relationships. The overall architecture consists of an input layer, one or more hidden layers and an output layer of neurons. Each neuron has a weight coefficient wi​ and a bias coefficient bi​, together with the input to the neuron zi​ and a nonlinear function such as the sigmoid function

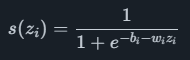
calculate an output value s(zi)s(zi​). Each neuron is connected to all neurons in the following layer, meaning that a neuron with multiple inputs will have a sum of multiple wizi‍​ terms in the exponent. The role of the sigmoid function here is often called an activation function, and other options besides the sigmoid are commonly used.

By adding multiple hidden layers between the input and output it is possible to create a very flexible model. With the model defined, data is passed through it and the result is compared to the actual value. By calculating the gradient of the error function it is possible to adjust the weights and biases towards a direction which will decrease the error. This process of optimization is called gradient descent. The whole process of adjusting the coefficients to the data is often called training the model, and the data used to do so is referred to as training data.

With all the flexibility offered, the biggest challenge is to avoid over-fitting the model to the data, meaning that the model becomes exceedingly good at describing the training data, but when presented with new observations it will struggle. Solving this is an open research question, but many useful techniques exist.

One example is to just pass a random sample of the data through the model at each iteration, resulting in the optimization technique referred to as stochastic gradient descent. Further, the data is often split into two parts, one which is used for training and another which is used for validation. The model is never allowed to use the validation set for training, but after a set number of iterations, the model is evaluated against the validation set. This way, it is possible to halt the training process as soon as the validation error is starting to increase. The benefit of this is that the model will be trained to be as specific as possible to the data while still remaining relevant to similar data not present in the training set.

With a large enough model and sufficient training data, it is possible to model very complicated structures. Examples of this is large language models which can mimic human language by predicting which word is most likely to come after the current sequence the model has received as input.

Time series and neural networks

To model a time series Yt​ using a neural network the pp lagged values Yt−1​,...,Yt−p​ are used as inputs and the neural network is trained to explain the current value Yt​. A forecast can then be created by using Yt​,...,Yt−p+1​ as inputs to predict Yt+1​. This can then be repeated in a recursive manner using the just forecast value as input, creating a forecast of the desired length.

How does Indicio fit a neural model?

A linear regression model can be fitted to data in a predictive manner, why a single model will almost always be sufficient. A neural network can end up with many different sets of coefficients stemming from the stochastic nature of SGD among other factors. To minimize the variance in the models, Indicio creates a number of models which are then averaged when making the forecasts.

‍