MIDAS

The Mixed Data Sampling (MIDAS) model is one of the mixed frequency models available in Indicio.

When forecasting a slower moving time series such as a monthly, quarterly or yearly one, there can be a great benefit to use high frequency indicators to provide more up to date information about how what is happening in the economy.

For example, say that we want to forecast GDP which is only available a set number of days after each quarter. We may have stock indices and other indicators which are released on a daily, weekly or monthly basis. If we are nearing the end of the quarter, we will have a lot of data available which describes what happened inside the first quarter that we want to forecast. A mixed frequency model such as MIDAS is able to use these time series of varying frequency together to create a forecast of the variable of interest.

The most basic MIDAS model is the one referred to as Unrestricted MIDAS which in the case of a quarterly main variable with a single monthly indicator will take on the form

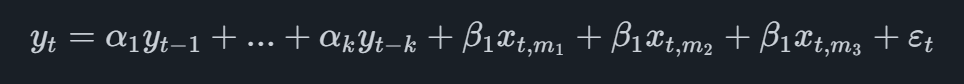
where the indicator variable has the subscript t,mi​ where mi​ is referring to the i'th latest monthly observation available. For example, if we were to forecast Q2 and we have monthly data of the indicator available up until May, we would add the observations of March, April and May into the equation.

In some cases we may have a quarterly or even a yearly main variable, and perhaps weekly or even daily indicators. This results in a very large number of parameters to be estimated, which may both make the estimates unstable and increase the risk of over-fitting the model to the data. The MIDAS model remedies this by using a polynomial lag function.

A polynomial lag function is some function which can produce a very flexible output but has a small number of parameters. If we have 30 lags when mapping a daily indicator to a monthly main variable, the polynomial allows the model to just employ a small number of flexible parameters which can create a function from which the individual daily parameters can be extracted. This results in parameters following a more or less smooth shape.

The intuitive explanation of why this works is that if we have a daily indicator which has a small effect in the beginning of the month and a larger effect at the end, the polynomial will be able to create a smooth set of parameters which start low and increase as the end of the month draws near.

‍

‍