Finding what affects your markets is an arduous task. At Indicio, we have had discussions throughout the years with many industrial forecasters, supply chain managers, strategic planners, and one thing stuck out: the very common usage of correlation analysis to find relevant indicators.
As an example, Apple could use the number of law graduates passing the Bar in Iowa to forecast iPhone sales. As a matter of fact, they shared a 99.19% correlation between 2007 and 2013. This is an obvious spurious correlation that should be avoided at all costs. This article intends to prove with simple math why correlation is not trustworthy, and how Indicio solves the problem the appropriate way.

When dealing with time series data, it is common to observe a dependency between 2 observations proximate in time. We therefore simulate data with a very simple function, as represented here:


xt is a data observation that is dependent on its first lag xt-1 with a coefficient = 0.9 and a random error term t.
We can now calculate how an observation correlates with its first and second lags.
- Corr(xt,xt-1) = 0.78
- Corr(xt,xt-2) = 0.58
We obtain two fairly high coefficients. Following correlation analysis, we can deduce that the first and second lags both seem to play an important role to predict the simulated data. However, looking at the function above, xt was generated solely using xt-1. Consequently, we need to introduce the concept of partial correlation. Partial correlation is measured by taking into account the effect of another variable in the calculus.
Let’s illustrate with the same simulated data, but with a regression this time, as it is closely related to partial correlation as illustrated here:


The coefficient 0.869 associated with the first lag is highly significant and fairly close to 0.9, which is what we simulated. Hence, we observe its clear relevance to predict this data. However, now looking at the -0.058 coefficient associated with the second lag, we see that it is null with no significance. Despite a large correlation, the second lag is logically not useful to make predictions here, as we generated the data based on the first lag only.
Corr (xt-1) = 0.081
Once we account for the correlation between the observation and its first lag, there is not much information left to capture in the second lag. If we had followed the first correlation results, we would probably have predicted this variable using both lags. We now showed that this methodology is wrong.
Correlation analysis being out of the picture, an important question remains: How should we find good leading indicators? There are so many out there and you need to find the right ones. At Indicio, we entrust this task to Lasso. Let’s take another easy math example.

We generated some data y that depends on 2 indicators covariates 1 and 2 and added 20 random noise indicators. They are not needed but in the real world we would not know this and would try to pull out 1 and 2 and leave out the noise. This is basically looking for a needle in a haystack. We made the problem even harder by setting high correlation between x1 and x2, so that it would be hard to disentangle the effect of the signal indicators.
We trained the model with 250 data points and kept 250 for testing.

Using the basic correlation measure on the left plot, we can see that correlation remains stable as we add more data and it understands that the noise should not be correlated and that our signals are important. On the right plot, Indicio directly suppresses the noise (green and red) from 25 observations. The non-influence from the noise is automatically detected and set to 0. Although wobbly early in the process, our signals stabilize eventually as we add more observations. Comparing these 2 plots, it is easy to consider correlation analysis perfectly capable of detecting relevant information and excluding irrelevant noise. However, the demonstration above showed that correlation analysis may not be trusted.
The strength of Indicio is to combine partial correlation when searching for indicators and Lasso regularization for noise isolation.

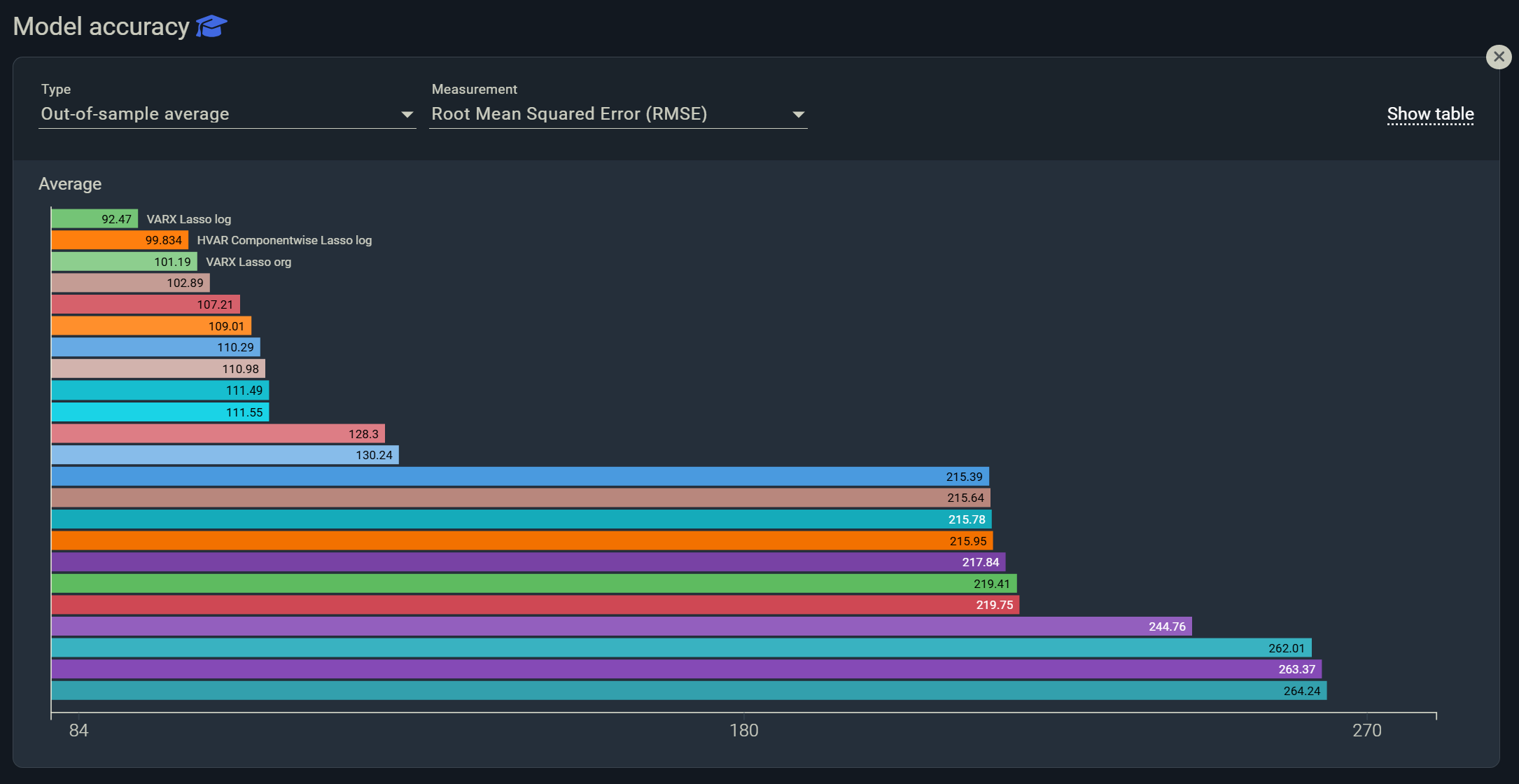
Inspecting strict forecast performances measured by RMSE on the plot above, Indicio and Lasso are immediately much more accurate than a regular regression. It takes many observations for the regular least square regression to decrease forecast error while Lasso does it immediately, with very few observations. The reason why it performs so well is its shrinkage power.
It penalizes useless coefficients to make the model more stable and thus more accurate. This is what Indicio’s high forecast accuracy relies on: correctly identified variables with partial correlation, combined with robust models enhanced by Lasso.